Table Of Content

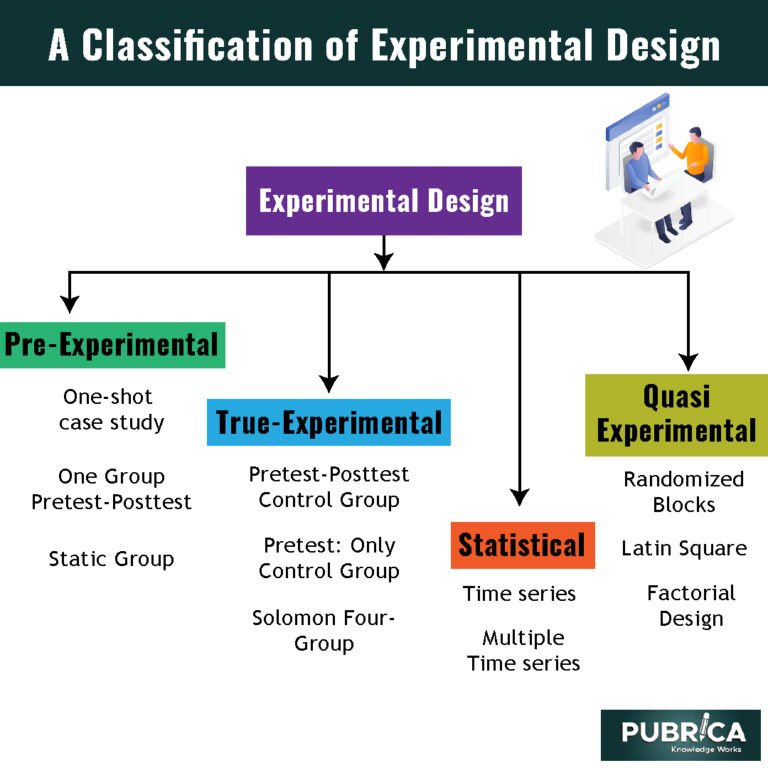
Although the sex of the patient is not the main focus of the experiment—the effect of the drug is—it is possible that the sex of the individual will affect the amount of weight lost. This is a paired design, which is the most simple form of randomized complete block design. The widespread use of the statistically in-valid RTTG design, which is not found in any reputable textbooks, may account for a substantial fraction of the observed irreproducibility. People, places, species and scientific procedures have names which can be used to identify and describe a subject or a procedure. Experimental designs also have names; “Completely randomised”(CR), “Randomised block”(RB), “Latin square”, “Matched pairs” etc.
Completely Randomized Design
So far we have discussed experimental designs with fixed factors, that is, the levels of the factors are fixed and constrained to some specific values. In some cases, the levels of the factors are selected at random from a larger population. In this case, the inference made on the significance of the factor can be extended to the whole population but the factor effects are treated as contributions to variance. Here we have two pairs occurring together 2 times and the other four pairs occurring together 0 times. Therefore, this is not a balanced incomplete block design (BIBD).
Statistical Analysis of the Latin Square Design
The foundational concepts of blocking date back to the early 20th century with statisticians like Ronald A. Fisher. His work in developing analysis of variance (ANOVA) set the groundwork for grouping experimental units to control for extraneous variables. Too many pre-clinical experiments are giving results which cannot be reproduced.
Subjects
An assumption that we make when using a Latin square design is that the three factors (treatments, and two nuisance factors) do not interact. If this assumption is violated, the Latin Square design error term will be inflated. For most of our examples, GLM will be a useful tool for analyzing and getting the analysis of variance summary table. Even if you are unsure whether your data are orthogonal, one way to check if you simply made a mistake in entering your data is by checking whether the sequential sums of squares agree with the adjusted sums of squares. Another way to look at these residuals is to plot the residuals against the two factors.
The row effect is the order of treatment, whether A is done first or second or whether B is done first or second. So, if we have 10 subjects we could label all 10 of the subjects as we have above, or we could label the subjects 1 and 2 nested in a square. This is similar to the situation where we have replicated Latin squares - in this case five reps of 2 × 2 Latin squares, just as was shown previously in Case 2.
The term experimental design refers to a plan for assigning experimental units to treatment conditions. The RB design, is already widely used in studies involving pre-weaned mice and rats11. So each is regarded as a “block” and one of the treatments, chosen at random, is assigned to each pup within the litter.
1 Powergain of blocking?
So what types of variables might you need to balance across your treatment groups? Blocking is most commonly used when you have at least one nuisance variable. A nuisance variable is an extraneous variable that is known to affect your outcome variable that you cannot otherwise control for in your experiment design. By extension, note that the trials for any K-factor randomized block design are simply the cell indices of a k dimensional matrix. Implementing blocking in experimental design involves a series of steps to effectively control for extraneous variables and enhance the precision of treatment effect estimates. The objective of the randomized block design is to form groups where participants are similar, and therefore can be compared with each other.
Randomized Block Design
You can obtain the 'least squares means' from the estimated parameters from the least squares fit of the model. My guess is that they all started the experiment at the same time - in this case, the first model would have been appropriate. Here is a plot of the least squares means for Yield with all of the observations included. Above you have the least squares means that correspond exactly to the simple means from the earlier analysis. Imagine an extreme scenario where all of the athletes that are running on turf fields get allocated into one group and all of the athletes that are running on grass fields are allocated into the other group. In this case it would be near impossible to separate the impact that the type of cleats has on the run times from the impact that the type of field has.
Differential pulse voltammetric assessment of phthalate molecular blocking effect on the copper electrode modified by ... - ScienceDirect.com
Differential pulse voltammetric assessment of phthalate molecular blocking effect on the copper electrode modified by ....
Posted: Sat, 01 Apr 2023 08:14:12 GMT [source]
1.1 Power for completely randomized design
(The exact proportion would be chosen randomly.) You would have 5 oven runs for each temperature; this could help you to account for variability among same-temperature oven runs. In a completely randomized $2\times2$ factorial layout (no blocks), you would completely randomly decide the order in which the breads are baked. For each loaf, you would preheat the oven, open a package of bread dough, and bake it.
For a complete block design, we would have each treatment occurring one time within each block, so all entries in this matrix would be 1's. For an incomplete block design, the incidence matrix would be 0's and 1's simply indicating whether or not that treatment occurs in that block. It looks like day of the week could affect the treatments and introduce bias into the treatment effects, since not all treatments occur on Monday. We want a design with 3 blocking factors; machine, operator, and day of the week. The choice of case depends on how you need to conduct the experiment. If you are simply replicating the experiment with the same row and column levels, you are in Case 1.
These can be found in textbooks which describe the characteristics and uses of each design13. However, none of the papers in the above survey mentioned either the CR or the RB design by name, although these are the only designs suitable for general use. Instead of a single treatment factor, we can also have a factorial treatmentstructure within every block.
Positive results will only be detected if the blocks give similar results, as assessed by statistical analysis11,12. Montgomery9,p 12 even suggests that blocking is one of the three basic principles of experimental design, along with “replication” and “randomisation”. In the RB design, the experiment is split up into a number of independent “blocks” each of which has a single subject assigned at random to each treatment.
In general, we are faced with a situation where the number of treatments is specified, and the block size, or number of experimental units per block (k) is given. This is usually a constraint given from the experimental situation. And then, the researcher must decide how many blocks are needed to run and how many replicates that provides in order to achieve the precision or the power that you want for the test. Crossover designs use the same experimental unit for multiple treatments. The common use of this design is where you have subjects (human or animal) on which you want to test a set of drugs -- this is a common situation in clinical trials for examining drugs.
This is not valid because each treatment group will occupy a different micro-environment, the effects of which may be mistaken for treatment effects, leading to bias and irreproduciblity. In the previous example, gender was a known nuisance variable that researchers knew affected weight loss. If we choose one of the RCB Design Structures, Temperature effects are completely randomized at the Run level. Recipe is nested within temperature and has a different error structure than temperature, because each dough appears within each run. The contrasts looking at recipe and recipe by dough non-additivity (interaction) do not have run-to-run variability in them. Technically, this is called variously a split-plot design structure or a repeated-measures design structure.
To address nuisance variables, researchers can employ different methods such as blocking or randomization. Blocking involves grouping experimental units based on levels of the nuisance variable to control for its influence. Randomization helps distribute the effects of nuisance variables evenly across treatment groups.


No comments:
Post a Comment